BIG and Geometry

By suggestion of a friend driven by sheer curiosity I went to discover a small piece of software which comes with MAC OSX called Grapher (Applications \ Utiilities). Grapher is able to create 2D and 3D graphs from simple and complex equations. Going through the "Examples" provided you can find one called Toroid that results from the expression given above. It immediately brought to my mind the image of BIG's Danish Pavilion at Shanghai.

Is this another "one liner" by Ingels explained after its conception?

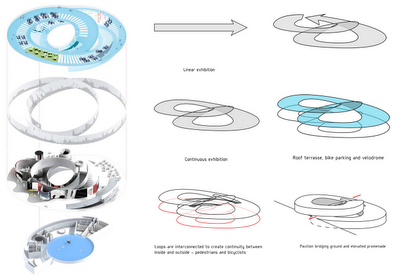
Of course Ingels has delved into geometry in the conception of his buildings some other times, even if quite inconsequently - geometrically and generatively, that is. More striking than the images created is the sense that some opportunities to re-explore geometry as a space generator are lost somewhere along the way.

Image sources:
domus
dezeen 

As a side note I would like to divulge a small plug-in for Rhino aptly called Math. What it does is: it calculates smooth degree 3 curves and surfaces based on parametric equations. It comes with a fairly diverse library, complete with Moebius strips and a Klein surface. The thing is, it works with cartesian, or rectangular functions. So, because I don't know how to convert polar functions like the above, I still haven't been able to construct it in Rhino.